
多様体学習とは、あるデータセットの次元削減を行うために、特徴数を削減する方法です。データ内に非線形の関係がある場合にも対応できます。
多様体学習アルゴリズムは教師なし学習の一種で、データセットを高次元空間に埋め込まれた低次元の多様体として記述しようとする物です。多様体とは、例えば1枚の紙です。この紙は3次元空間に埋め込まれた2次元多様体と考えることができます。3次元空間で紙を回転させても、方向を変更しても、平面であることに変わりはありません。この操作は線形埋め込みに似ています。紙を曲げたり、丸めたり、ねじったりする場合、2次元の多様体であることに変わりはありませんが、3次元空間への埋め込みはもはや線形ではありません。3次元空間を埋めるように歪曲されていても、多様体学習アルゴリズムで学習を行い、紙の基本的な2次元的性質を探し出せます。
多様体学習の概念をより明確にするために、まず多様体を定義するための2次元データを生成します。ここでは「NSRI」という単語の形でデータを作成する関数を定義します。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import pairwise_distances
from sklearn.manifold import MDS
from mpl_toolkits import mplot3d
def make_text(N=1000,rseed=42):
fig,ax=plt.subplots(figsize=(4,1))
fig.subplots_adjust(left=0,right=1,bottom=0,top=1)
ax.axis('off')
ax.text(0.5,0.4,'NSRI',va='center',ha='center',weight='bold',size=85)
plt.grid
fig.savefig('NSRI.png')
plt.close(fig)
from matplotlib.image import imread
data=imread('NSRI.png')[::-1,:,0].T
rng=np.random.RandomState(rseed)
X=rng.rand(4*N,2)
i,j=(X*data.shape).astype(int).T
mask=(data[i,j]<1)
X=X[mask]
X[:,0]*=(data.shape[0]/data.shape[1])
X=X[:N]
return X[np.argsort(X[:,0])]
def rotate(X,angle):
theta=np.deg2rad(angle)
R=[[np.cos(theta),np.sin(theta)],[-np.sin(theta),np.cos(theta)]]
return np.dot(X,R)
def random_projection(X,dimension=3,rseed=42):
assert dimension >= X.shape[1]
rng=np.random.RandomState(rseed)
C=rng.randn(dimension,dimension)
e,V=np.linalg.eigh(np.dot(C,C.T))
return np.dot(X,V[:X.shape[1]])
X=make_text(1000)
colorize=dict(c=X[:,0],cmap=plt.cm.get_cmap('viridis',4))
plt.scatter(X[:,0],X[:,1],**colorize)
plt.axis('equal');
plt.show()
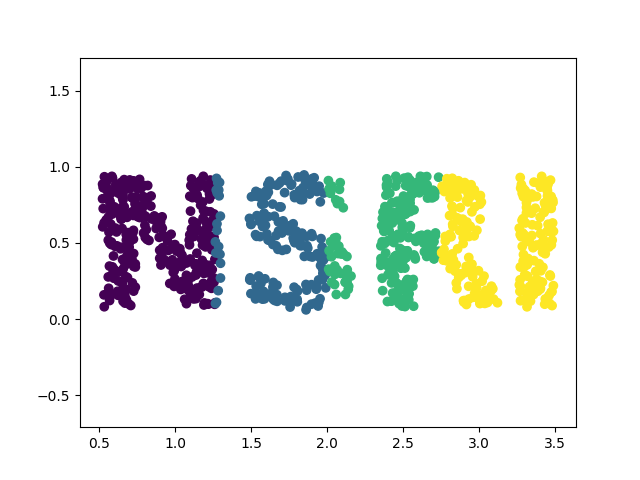
このようなデータを見ると、x値とy値はデータの最も基本的な記述方法ではないことがわかります。データを拡大、縮小、回転を行っても、データは「NSRI」に見えます。例えば、回転行列を使用して、データを回転するとxとyの値は変化しますが、データそのものは基本的に変わりません。文字が回転した画像は以下の通りです(上のコードでrotate()関数を実行する)。

つまりこれは、xとyの値が必ずしもデータの関係にとって本質的ではないことを示しています。この場合の本質とは、データセットの各ポイント間の距離です。これを表すには、距離行列を用いるのが一般的です。Nポイントの場合、要素(i,j)がポイントiとポイントj間の距離を持つN✕N配列を作成します。効率的な実装であるscikit-learnのpairwise_distances関数を使用して、もとのデータに対して距離行列を作成します。この距離行列は回転と平行移動で不変であり、この距離行列からMDSと呼ばれる多次元尺度構成法を用いてデータを復元することができます。

